数学嫌いだった理系博士はどう克服したか『なっとくする数学記号』
この記事は約 6 分で読めます
今回の書評は『なっとくする数学記号 (なっとくシリーズ)』です。
記号が生まれた背景やストーリーを知ろう
あなたは数学が嫌いですか?私は理系博士ですが、正直数学は今でも苦手です。
私は高校で数学が嫌いになりました。理由は、無味乾燥に見える式がつらつらと教科書に書かれていたからです。数式が暗号にしか見えませんでした。
高校の授業で数学の先生がどう教えていたのかはあまり覚えていません。ただ先生の言うことはやたら細かく、つまらなかったという印象だけが残っています。あなたもそうではありませんでしたか?
数学が数式のオンパレードになったのには理由があります。数学者の桜井進氏はニコラ・ブルバキというフランスの数学者集団に原因があると指摘しています(『夢中になる!江戸の数学』集英社文庫 (2012) pp.70 – 71 )。
ブルバギは何十巻にもなる数学の教科書をまとめる際に、その方が合理的だという理由から極力数式にしたといわれています。フランス人の美的感覚がそうしたのでは?とも考えられます。
これは 20 世紀に入ってからの話です。それ以前の数学の証明は文章が主体だったと桜井氏は指摘しています。
本書は数学にもっと興味を持ってもらうために、数学記号がどのようにして生まれたのか、なぜそのような表現になったのかを解説しています。学生であれば数学の参考書として、社会人には教養として数学に触れて欲しいという想いが込められています。
取り扱い範囲は広く、プラスマイナスの初歩的な算数の話から、代数、微分積分、集合、幾何学、論理学、と大学の数学にまで及びます。
極力数式は使わないという本書の方針から、記号だけの展開は意識して避けています。図解を入れたり、ルートなどの記号がなぜ今の形になったのか、当時の数学者のエピソードを交えるなど著者の努力が見えます。
このようにストーリーを語ることで「数式がただの記号の並びではない」ことを著者の黒木氏は何度も主張しています。
終盤はさすがに数式の展開が目立ちますが、大学レベルの内容となればやむを得ないでしょう。
文庫本ではないので気軽に読める本ではありません。しかし本書は 2001 年に出版されたロングセラーです。他の数学の解説本にはないアプローチに定評があるのでしょう。
数式は数学語という表現だった
本書を通じてわかったことがあります。それは「数式はある種の言葉による表現である」ということでした。
私の経験を 1 例を紹介します。
私は高校数学で「微分=傾き」としか教わりませんでした。私は馬鹿なので「傾きってなんなんだ?」とずっと思っていました。
この疑問はそのままに、大学を卒業して大学院に進みました。さすがに数学をしっかりやらないといけないと思い、本書をはじめとする数学の本を読んだところやっと理解しました。
微分はある点での変化量を求めることです。この言い方だけでは難しいですよね。例えば「車の速度(時速)」は、ある時点での「 1 時間で動ける距離」です。
走っている車は 1 時間後に、元の場所とは違うところにいますね? 1 時間で車のいる場所が「変化」しています。

図で解説しましょう。横軸を時間、縦軸を距離として時速 20 km と時速 60 km の水色の直線を引きます。 1 時間に移動できる距離が大きい(時速が大きい)ほど矢印は横ではなく上向きになります。この上向き矢印が「傾き」です。
この傾き(角度)が大きいほど速く、図の左にあるように移動距離も多くなります。この例では時速 20 km より60 km の方がよりグラフの上に行ってます。時速 60 km の方が短時間で遠くにいけるので納得できますね。
このように 1 時間に 60 km, もしくは 20 km 移動できる変化の量が微分値です。また、どれくらいの変化なのかを求める作業を微分と言うのです。微分した値をわたしたちは日常的に使っているのです。
しかし文章で書くとどうしても長くなってしまいます。
具体的な事例はこれ以外にもあります。たくさんの事例から共通する考え方を抜き取り、グラフで説明すると「傾き」という言い方になる。さらに西洋記号を使って表現すると dx/dt となるのです。
雑巾をしぼるように余計な表現を出し切り、残った部分が数式です。
このように具体的な内容から概念を抜き取り数式にすることを抽象化と言います。抜き取られた数式もあくまで言葉(文章表現)の一部なので、私には「数式=数学語」という言い方がしっくりします。
数学語は英語のような外国語の1つで、日本語とは違うものです。学校の授業だけで英語ができないように、学校の授業だけでは数学に精通するのは難しいのでしょう。雑巾をしぼりきった後の最小限の内容しか教えないからです。
数学記号にアルファベットやギリシャ文字を使うのは、たまたま西洋の人たちが使っていた表現を輸入したからです。江戸時代に確立された和算をそのまま使っていれば、日本の数学は記号の替わりに漢字を使っていたかもしれません。
私は様々な本を通じて具体例から数学的な表現をやっと理解しました。しかし今でも電気工学や物理で出てくる高度な数学は理解できません。恥ずかしいし悔しいですが、仕事や生活に支障はないため良しとしています。
数学を理解するには想像力が必要です。著者も式だけで展開することに疑問を投げかけています。引用させていただきます。
記号というのは、書くことを節約するだけでなく、概念を表現するものでもあり、現代のロゴマークと同じくメッセージ性の高いものである。
このように、ロゴマークだと思うと親しみが持てるかもしれませんね。
エクセル計算から数式をイメージする
数式や記号の概念がイメージできないのであれば、手を動かしてみるのも良いでしょう。
といっても紙と鉛筆を使う必要はありません。現在はエクセル(表計算ソフト)という便利なツールがあります。計算過程を見える化して、数式をイメージしてみましょう。
本書から 1 つ例を紹介します。シグマ計算 (p.43) です。
この記号は 18 世紀に活躍した天才数学者のオイラーが発案しました。複数の値の合計をギリシャ文字のシグマ (Σ) で簡略化しました。この計算をエクセルで入力してみると図のようになります。
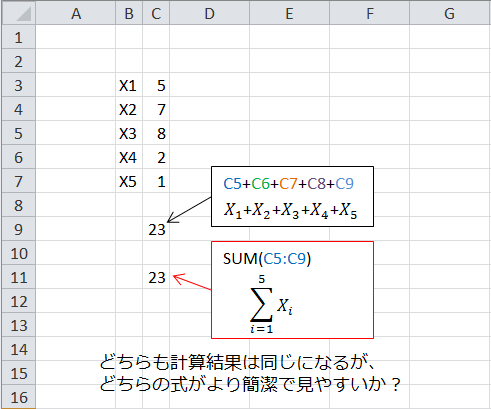
図には 2 種類の式があります。 5 つの値を個々に足す場合と、シグマを使って計算した場合で結果は同じです。しかし 1 つずつ足す計算式を入力するよりも、エクセル関数の SUM を使ったほうが式の入力は楽ですね。
このように、オイラーが提案したシグマ(エクセル関数の SUM )を使うと計算が楽になるメリットがあります。この例では式が単純ですが、物理や他の世界ではもっと難しい式が出てくるので、シグマの威力はより大きくなります。
プログラミングをやっているとこういう事例は他にもあります。エクセルを使って数学を解説している本も出版されています。ご興味があれば読みながら計算して式の意味を理解するのもいいでしょう。
このように、数学は身近にあるものです。「数学を勉強して何の役に立つのか?」と言うのは簡単ですが、もう少しリラックスして接してみるのはいかがでしょうか。

