技術や数学にも精通していた偉人『教養として知っておきたい二宮尊徳』
この記事は約 7 分で読めます
今回の書評は『教養として知っておきたい二宮尊徳 (PHP 新書) 』です。
合理的なアドバイスと多動力で地方財政を再建
二宮尊徳が理系人間だったことを知りませんでした。
かつてはどこの学校にもあった「薪を背負って本を読む二宮尊徳像」、私も見たことはありません。 1981 年生まれの私ですら見たことないのに、さらに下の世代には二宮尊徳が何者かはわからないことでしょう。
著者は、かつて道徳の教科書に必ず出てきた二宮尊徳(二宮金次郎)の業績が忘れられてしまう危惧から本書を執筆しました。私も歴史上の偉人である二宮尊徳について知りたくて購入しました。
著者の松沢氏は元神奈川県知事。神奈川県民の私としてはどういう目線でまとめられたのか、とても気になりました。
尊徳が生涯を通じてやった主な仕事は、農村改革、藩や武家の復興(今で言う財政破綻した自治体の建て直し)でした。ただし政治的な動きだけでなく、きわめて合理的でかつ実践的な建て直しをしました。
尊徳が実際にとった行動の一部はこのようになっています。
- 過去の年貢帳を調べて収益実態を調査
- 田畑の測量(年貢量の推定、現地調査)
- 具体的な再建計画(マニフェスト)を提案し藩主を説得
- 貧しい人を自立させるためのお金の貸付(現在の金融業)
- 飢饉を予測した農作物生産種の指示や米相場での米の売買
- 信用組合の設立
今でも通用する立て直し策を江戸時代後期にやり、かつ実績をきちんと上げたのです。
具体的な立て直しの話はぜひ本書を読んでみてください。尊徳の活動範囲は関東一円とそれほど広くありません。しかし多くの地方から引き合いをうけ、反対勢力と折り合いをつけながら着実に地方を立て直す。そんな熱い話に意外にも私は引き込まれてしまいました。
本書は幼少期の尊徳の苦労話から始まるサクセスストーリーです。創意工夫を常に怠らなかった尊徳の姿に、ひとりの技術者として感動がありました。
近年は渋沢栄一の『論語と算盤』が再び脚光を浴びています。おそらくメディアアーティスト落合陽一氏の影響かもしれません。明治時代に生きた渋沢栄一は二宮尊徳の時代からあまり離れてないため、強く影響を受けているはずです。
尊徳の名言を1つ引用しましょう。
経済を伴わない道徳は戯言であり、道徳を伴わない経済は罪悪である
渋沢栄一が言った論語は道徳、算盤は経済のことです。時代に合わせてうまく伝わる表現を選んだのでしょう。
このように尊徳の死後、後世の経営者・実業家・経済人や政治家にどのように影響を与えたのかについてもページを割いています。また尊徳の教えが世界中で広まってきている様子についても具体的に書かれています。
枡を設計・標準化して年貢の不公平を無くした
本書を取り上げた最大の理由、それは二宮尊徳の技術者としての側面です。
彼は近代工業でいうところの「標準化」を進めた人でもありました。理系人間の私にとって驚くべきストーリーだったので、掘り下げて紹介させてください。
文政三年 (1820) の小田原藩。当時年貢の測量には 18 種類の異なるサイズの枡が使われていました。そのため藩の役人が正規の量以上の米を請求するなど不公平な年貢の取り立てが行われていました(同書 kindle 版 位置 No. 416 付近)。
この事態を改善すべく、尊徳は「 3 回で 1 俵の米が量れる枡」を設計しました。この枡のおかげで公平な取り立てができ、実質的な減税ができるようになりました。
枡の設計なんて簡単なのでは?とお考えでしょうか。これは明治以前の話です。
難しいので図も使って説明しましょう。
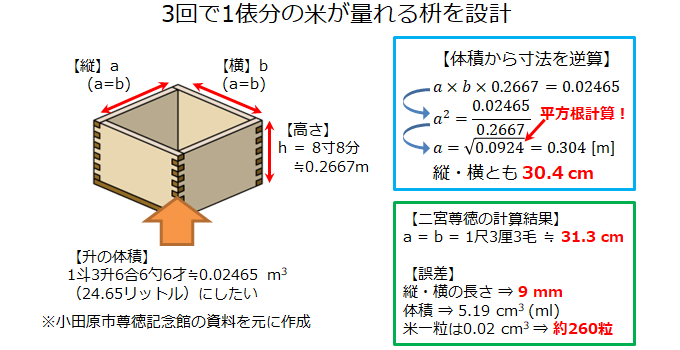
設計したい枡は私たちも見たことのあるシンプルな四角形です。そのため体積は「縦×横×高さ」というシンプルな式で計算できます。
ただし、ここでやりたいことは枡の体積を計算したいのではありません。「ある体積を得るには、枡の寸法をどうすれば良いか?」ということです。言い換えると、体積から枡の縦、横、高さを逆算したい。
これは理系的には立派な設計行為です。ある目的を達成するためにパラメータを決定する、これが設計です。
3 回で 1 俵とするには、枡の体積を 1 斗 3 升 6 合 6 勺 6 才(約 0.02465 m 3 = 24.65 リットル)にしたい。決めたい寸法は縦、横、高さですが、正方形なので縦と横は同じ長さで問題ありません。つまり、 1 辺の長さと高さの 2 つがわかればよいのです。
尊徳は高さを 8 寸 8 分(約 26.67 cm) と先に決めました。米の字を分解した八の字が理由です。
そんな決め方で良いの?と思われるでしょう。現在の開発環境でこんな決め方をしたら間違いなく上司に怒られます。
設計は根拠を説明できればとりあえず大丈夫です。江戸時代当時の状況であればかまわないでしょう。大切なのは目的です。枡を作り百姓を助け、財政を安定化させることです。
この高さの値と体積の計算式から1辺の長さを逆算しました。中学数学で学ぶ初歩的な方程式ですね。尊徳の答えは1尺3厘3毛(約30.4cm)でした。
尊徳の計算結果と現在のメートル法による計算結果を比較しました。その結果、 1 辺の誤差は 9 mm, 体積は米粒で言えば約 260 粒の誤差でした。あくまでも理論上の誤差ですが、江戸時代の当時にここまで正確に設計したことには驚きでした。
これだけ正確な枡があれば、お百姓さんはさぞかし助かったことでしょう。この枡のおかげで小田原藩内では年貢の支払いが「標準化」され、誰でも同じ量の年貢を納めることができるようになりました。
他にも理系的なエピソードが出てきます。
住み込み奉公先の家計を立て直すために、台所で使う火の量をそのままで消費する薪の数を減らすアドバイスをします。これは今で言う最適化問題で、理系的な発想が必要です。
またすでに解説したように、年貢量を推定するために土地の測量もしました。正確な計算をするためには数学的な知識が必須でした。
このような視点で読んでいただくのがおすすめです。違った二宮尊徳の一面を知ることができるでしょう。
和算のベストセラーから数学を独学した?

枡の寸法設計に平方根の計算が出てきました。尊徳はどのように平方根の計算を克服したのでしょうか?
私は小田原にある資料館にて担当者様と雑談したのですが、江戸時代にどうやって計算していたのか?不思議でした。本書でも「尊徳は開平法(平方根の計算)を独力で勉強し」としか書かれていません (kindle 版位置 No. 1336 付近)。
ところがさらに自分の無知を知らされます。江戸時代にはすでに高度な数学があったのでした。
まず私は「江戸時代の数学=和算」だと思い、和算の大家・関孝和(せき たかかず)から調べました。安易な発想かもしれませんが、和算についてそれしか知りませんでした。
二宮尊徳が関孝和にどう計算すればよいのか教えてもらおうとした、そんな仮説を立てました。ところが両者は生きた時代が違いました。
- 二宮尊徳: 1787 – 1856 (外部リンク:二宮尊徳 – Wikipediaより)
- 関孝和: 1642 – 1708 (外部リンク:関孝和 – Wikipediaより)
二宮尊徳が生まれるはるか以前に関孝和は他界しています。私の仮説はあっけなく崩れました。
さらに調べたところ、わかりました。
和算家の吉田光由(よしだ みつよし)が1627年に塵劫記(じんこうき)という和算の本を出版しました。なんとそこには平方根の計算方法が書かれていたのです(岩波文庫版 (1977) p.240 )。
さらに当時の枡の寸法と体積の計算(同 p.140 )、土地面積の計算方法(検地)についても取り扱われています。尊徳のやろうとしていたことは既に出版されていたことになります。
塵劫記は出版当時ベストセラーになりました(桜井進『夢中になる!江戸の数学』集英社文庫 (2012) より)。出版から 100 年以上経っていましたが、尊徳は入手して独学し、和算にも精通していた可能性が高いのです。
尊徳が読書家だったことは本書にも説明があります(同書 kindle 版 位置 No. 188 付近)。ただ勉強しただけでなく、「座学より実学」という尊徳の信念から枡の設計に応用した。
このように、尊徳が数学を駆使して農村改革や財政再建したのは納得できます。
だとすると次の疑問が出てきます。どうして二宮尊徳よりも前に誰も枡の標準化をやらなかったのか?
尊徳が枡の設計をしたのは塵劫記の出版から 100 年以上経ってからです。気づいていたけど誰も発案しなかったのか、役人の利権が絡んでいたのか。さらに想像は膨らみます。

